أنت لا تكره الرياضيات: أنت تكره مادة الرياضيات
الكثير من الناس ينفرون من أي تعبير رياضي أو تمثيل هندسي بحجة أنهم يكرهون الرياضيات أو يخافون منها، ويستندون بذلك إلى فشلهم الدراسي في مادة الرياضيات (وربما المواد التي تستخدم فيها الرياضيات بشكل صريح وكثيف.) والحقيقة أن الصورة المطبوعة في عقول الناس عن الرياضيات تعود إلى طريقة تقديم هذا الفن في المنظومة التعليمية التقليدية؛ وهي كأنك تقدم طبقًا لذيذًا من الأرز على قطعة حفاض للأطفال (غير مستعملة) لشخص لم يجرب الأرز من قبل، الأمر الذي قد يجعله يكره الأرز طيلة حياته.
في هذه المقالة سأناقش باختصار أسباب نجاح المدارس في جعل غالبية الشعب تكره الرياضيات. وسأورد كيف أن الرياضيات هي أكبر بكثير من حفظ جدول الضرب وبعض المتطابقات لحل مسائل لا معنى لها خارج ورقة الامتحان؛ من أجل نيل بعض الدرجات الأكاديمية والحصول على شهادة لا تثبت شيء سوى للحمقى. الرياضيات التي نتعلمها خلال مرحلة التعليم الأساسي تشكل جزء صغيرًا من الرياضيات ككل، وهذا الجزء يقدم إلينا بأسوء الأساليب الممكنة وأقلها كفاءة.
الجواب غير مهم، القدرة على الإجابة هي المهمة
المكافئة على دقة الجواب وسرعته هي من أغبى الأمور التي يمكن فعلها في أي نظام تعليمي، ولسبب بسيط: لا يملك جميع البشر نفس القدرة على الاستنتاج، وبالتالي، الطلاب التي تستطيع الاستنتاج بسرعة من خلال مراقبة الأنماط يمكنها إدراك العملية التجريدية بشكل أسرع، ومنه يمكنها الإجابة على الأسئلة قبل الطلاب الآخرين. هذا الأمر سيفقد الطلاب ذوي الاستنتاج البطيء الثقة بقدرتهم على تجاوز مادة الرياضيات، والكثير منهم سيصل إلى مرحلة ليضع وشم "فاشل في الرياضيات" على جبينه، مما سيجعله يعاني لاحقًا خصوصًا في المرحلة الإعدادية، وقد يصل الحال به إلى مغادرة المدرسة نهائيًا؛ وهو أمر قد يكون جيد. ولكن في نفس الوقت، هذا الطالب الذي كان من الممكن أن يقدم برهانًا رياضيًا على حدسية ريمان، الآن هو يعمل في صنع القهوة ليشربها الطلاب سريعي الاسنتاج عسى أن يستطيعوا التركيز في "الدراسة" داخل ذلك المقهى الطلابي المليء بالضوضاء.
نقطة مهمة أخرى يجب ذكرها وهي اختلاف الخلفية التعليمية لدى كل طالب. نسبة جيدة من الطلاب يتلقون تعليمًا مشابهًا لتعليم المدارس لكن خارج المدرسة؛ والعديد منهم يتلقون هكذا تعليم حتى قبل دخولهم للمدرسة (أنا شخصيًا منهم.) الطالب الذي يتلقى تعليمًا أكثر يعني أن لديه -في غالب الحالات- وقتًا أكبر من أجل أن يستوعب المفاهيم المختلفة (وربما من أجل أن يحفظ بعض القواعد عن ظهر قلب، دون أن يفهم من أين أتت.)، هذا الطالب بالضرورة سيكون لديه امتيازات تزيد من فرص بقائه في المدرسة، و"النجاح والتفوق" فيها.
هذه الاختلافات على الجانب العصبي والاجتماعي هي التي تحدد شكل سباق العلامات الذي يحدث في النظام التعليمي الرسمي التقليدي. الطالب الذي يتمكن من الإجابة بدقة وسرعة عاليتين سيكون "متفوقًا" و"ناجحًا" في الرياضيات، أما سواه فهو "فاشل" و"غبي" ويحتاج إلى الكثير من "فت الخبز". طبعًا هذا وأنا لم أذكر بعد العنف الذي يتلقاه الأطفال من أجل هذا السباق الساذج؛ سواء من قبل الكادر التعليمي أو من "أولياء أمر" الطفل، وقد يتطور لاحقًا إلى عقدة نفسية تؤثر على القدرة الاستيعابية للطفل. صَدَق من قال أن المدارس هي من تصنع الأغبياء.
جدول الضرب غير مهم، استيعاب عملية الجداء هي المهمة
نعم يا صديقي: جل ما تلقيته من عنف نفسي وجسدي بسبب عدم قدرتك على تذكر خانة معينة في جدول الضرب كان بلا جدوى. نعم، ذاك الجدول اللعين لا ينبغي جرده وحفظه. أساسًا جدول الضرب بصورته التقليدية ليس له أي معنى أساسي وقد فُرض عليك أن تحفظ كل خانة منه (مع إحداثياتها طبعًا) من أجل العادات والتقاليد فقط لا غير. عملية الجداء هي عملية تكرار لـ(جمع) عدد معين لعدد من المرات، فلأي عملية جداء يمكنك إجراء عملية الجمع هذه من أجل الحصول على الناتج (مثلًا 4 × 3 = 4 + 4 + 4). طبعًا، بالنسبة للأعداد الكبيرة، تصبح عملية الجمع هذه صعبة جدًا ولذا يمكننا تجزيء هذه الأعداد بطريقة معينة وإجراء عملية الجداء على هذه الأجزاء ومن ثم إعادة تركيب النواتج إلى ناتج موحد يمثل ناتج عملية الجداء الأصلية. ومع الممارسة يمكنك أن تختزل قسم كبير من هذه العملية وإجراؤه ذهنيًا (الأمر المكافئ عمليًا لحفظ جدول الضرب، لكن بطريقة أكثر آدمية، إن صح التعبير.)
لنفكر مجددًا: ما فائدة حفظ جدول ثنائي الأبعاد بشكل مستقل عن عملية الجداء نفسها (كما يحصل في المدارس)؟ سيخبرك أحدهم: هذا سيمكن الطالب من إجراء عمليات الجداء بشكل أسرع! وحينها سأخبره أن يعود لفقرة سباق العلامات في هذه المقالة ليقرأها مجددًا. طبعًا، جدول الضرب ليس العقبة الوحيدة في سباق العلامات المذكور، إنما مناهج الرياضيات (وغيرها) مليئة بمثل هذه العقبات التي ربما لا يستطيع تحديدها حتى الكادر التعليمي نفسه. فمثلًا لدينا التدوين الرياضي (تمييز الرموز وإعراب التعابير المختلفة، وربطها بالمفاهيم المجردة التي تمثلها)، المفاهيم الرياضية (ما هو العدد؟ ما هي النقطة؟ ما هو المستقيم؟ ما هي المساحة؟ ما هي المجموعة؟ ما هي المعادلة؟ ما هو التابع؟)، طرق الاستنتاج والربط (الرؤية التحليلية، عملية التجريد)، وغيرها من الخطوط العريضة. هذه القائمة تطول وتتضخم بتراكم الأمور غير المفهومة مع مرور السنين الدراسية لدى الطالب.
ما هي الرياضيات؟
حسب ما رأيت شخصيًا؛ جميع من يكره الرياضيات لم يتمكن من أن الإجابة على هكذا سؤال (طبعًا علي التأكيد بأنه غالبًا لا يكره الرياضيات بل مادة الرياضيات، الأمر الذي أشاركه به.) السبب يعود إلى أن معظم الطلاب -سواء أكانوا "ناجحين" في مادة الرياضيات أم لا- لا يدركون بالضبط ما هي الرياضيات. وهذا الأمر ينعكس على عامة الشعب، فغالبية الناس تظن أن الرياضيات هي "أرقام وحسابات"، بكلمات أخرى عامة الشعب تكافئ بين الرياضيات mathematics وبين الحسابيات arithmetics التي تكوّن جزء صغيرًا في الرياضيات (ومعظم تطبيقات هذا الجزء تمت أتمتتها عن طريق الكومبيوترات.)
في الواقع، حتى الرياضياتيين أنفسهم لم يتفقوا على تعريف واحد للرياضيات، لكن على الأقل يمكنهم تعريفها بطريقتهم الخاصة. ومن أكثر تعاريف الرياضيات سذاجة هي "ما يفعله الرياضياتيون" ومع سذاجة هذا التعريف إلا أن معظم طلاب المدارس لا يدركونه بشكل حقيقي. فالرياضياتيون ليسوا (بشكل عام) موظفين يقومون بإجراء الحسابات يوميًا لشتى الأغراض (خصوصًا في القرن الواحد والعشرين) أو حل المسائل التطبيقية المختلفة (العلماء والمهندسون هم من يقومون بذلك)، الحساب في الحقيقة نشاط بشري (وهو موجود عند حيوانات أخرى) حيث قام الرياضياتيون بتحليله منطقيًا وتجريده ودراسته صوريًا. نعم، التجريد والدراسة الصورية والتحليل المنطقي هي من أهم ما يفعله الرياضياتيون.
التعريف الأكثر شيوعًا للرياضيات هو "حقل معرفي يهتم بدراسة الكميات والأشكال والبنى والتغير". هذا التعريف الركيك نوعًا ما يعطينا فكرة بسيطة عن الأمور التي يتناولها الرياضياتيون. في المدرسة، نتعلم الحسابيات، وجزء بسيط من الإحصاء ونظرية الاحتمالات، وجزء جيد من الجبر التقليدي والهندسة الإقليدية وربما (في المراحل العليا) التحليل الحقيقي وحسبان التفاضل والتكامل والمصفوفات؛ الأمر يختلف حقًا من خطة تعليمية لأخرى.
الرياضيات هي أضخم من كل هذا بكثير، فحتى الحسابيات يمكنك إجراؤها بطرق أخرى لا يتم تعليمها بالمدارس، على سبيل المثال يمكنك استخدام قاعدة base للعد غير العدد 10. طبعًا أنا هنا لا أقول أن المدارس عليها تدريس كل شيء في الرياضيات (وهذا مستحيل عمليًا حتى في الجامعات)، ولكن على الأقل لنعطي الطلاب فرصة لتفهم ما هي الرياضيات فعليًا وماذا تدرس بشكل أساسي. ففي بلدي مثلًا معظم طلاب المرحلة الثانوية يظنون أن التحليل هو جزء من الجبر، بسبب أنهم يظنون أن الرياضيات تقسم إلى جبر وهندسة؛ بسبب أن المنهاج موزع في هذه الطريقة 🙂
النماذج الرياضية والمسلمات والمبرهنات والبراهين
بشكل ما، يمكننا اختصار الرياضيات في عبارة "عملية وصف متراصة منطقيًا"، تصف هذه العملية الأنماط التي يمكن أن يستوعبها العقل البشري عن طريق تجريد هذه الأنماط، وهذا الوصف يتمثل بنتائج رياضية معينة، تسمى بالحدسيات أو النظريات، أو مبرهنات في حال تم تقديم برهان عليها انطلاقًا من مجموعة من المسلمات (وهي شروط معينة يُفترض أنها صحيحة) والمبرهنات الأخرى. طبعًا حتى عملية البرهان وتحديد المسلمات هي موضوع تحت دراسة الرياضيات، ولو أنه ينتمي كذلك إلى فلسفة الرياضيات (وهي فرع من الفلسفة يعنى بدراسة طبيعة الرياضيات وحالتها الإبستيمولوجية).
طبعًا حفظ البراهين وكأنها ضرب من الشعر لن يجعل منك رياضياتيًا، إنما استيعاب عملية البرهنة وطرق البرهان المختلفة هو ما سيجعلك كذلك (أو على الأقل سيكون بداية الطريق). ربما قد جُبرت في مرحلة دراسية معينة أن تحفظ بعض البراهين عن ظهر قلب، أو أن تحفظ بعض المبرهنات من أجل حل المسائل دون فهم كيف ومن أين أتت هذه المبرهنات (وكيف تم برهانها). لنأخذ مبرهنة فيثاغورس مثالًا: يستطيع طلاب المرحلة الثانوية (في بلدي على الأقل) كتابة العلاقة الرياضية المستخرجة منها، ولكن تقريبًا لا أحد منهم قادر على برهانها. مع أنها من أشهر المبرهنات الرياضية ويوجد عليها إلى حد اللحظة حوالي 370 برهان رياضي؛ حيث تختلف هذه البراهين بدرجة الصعوبة والتعقيد والخلفية الرياضية اللازمة لاستيعابها والتأكد من صحتها.
تنص مبرهنة فيثاغورس على أن "في أي مثلث قائم، مربع وتر المثلث يساوي مجموع مربعي الضلعين الآخرين من هذا المثلث". طبعًا من أجل فهم هذا النص، عليك فهم معنى كل من: "مثلث قائم"، "مربع"، "وتر"، "مجموع"، و"ضلع". سأفترض أن هذه المصطلحات مألوفة لديك إلى درجة ما، وإلا فشرحها هنا سيتحول هذه المقالة إلى كتاب.
معظم الطلاب يحفظون هذه العلاقة:
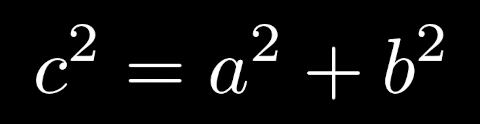 علاقة فيثاغورس
علاقة فيثاغورس
لكن لا أتوقع أن غالبهم سيتذكر أن هذه العلاقة خرجت من هذا الشكل (الذي هو تمثيل مرئي لنص مبرهنة فيثاغورس):
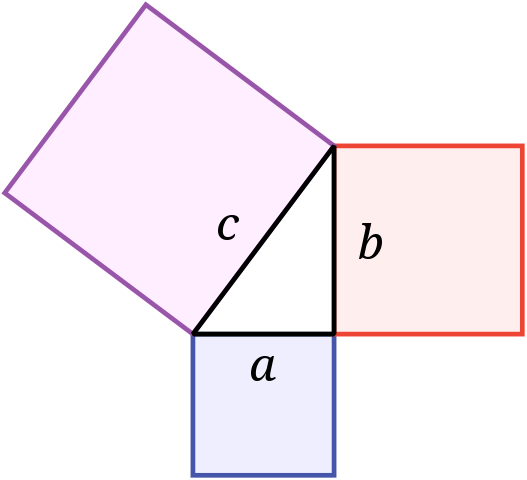 مبرهنة فيثاغورس
مبرهنة فيثاغورس
نعم. معظم الطلاب لا تدرك أن مربع عدد ما يمكن تمثيله هندسيًا بمساحة مربع طول ضلعه يساوي هذا العدد. مع أنهم تعلموا أن مربع العدد هو حاصل جداء العدد مع نفسه، وتعلموا أن المساحة هي عدد النقاط المحصورة ضمن مضلع ما. عندما يكون هذا المضلع مستطيلًا، فهذه المساحة (عدد النقاط) تمثل جداء طول (عدد نقاط) الضلع الطويل من المستطيل مع طول (عدد نقاط) الضلع القصير من هذا المستطيل؛ أي أنها تكرار لعدد نقاط إحدى الضلعين بعدد من المرات يكافئ عدد نقاط الضلع الآخر، أو بكلمات أخرى، هي مسح (نسخ وسحب بمقدار نقطة واحدة) إحدى الضلعين على طول الضلع الآخر؛ الأمر الذي سيملئ هذا المستطيل بالنقاط التي عددها يساوي مساحة هذا المستطيل. في حالة المربع، جميع الأضلاع متساوية بالطول وبالتالي فالمساحة هي بالضرورة جداء طول ضلع المربع مع نفسه، أي مربع عدد النقاط (ومنه نعود إلى بداية الفقرة). التدريب اللازم للوصول إلى هكذا نتائج ترابطية بسيطة لا يتم في المدارس إلا في حالات نادرة جدًا، أما في غالب الأحيان فعلى الطلاب أن يصلوا إلى هذه النتائج بشكل اختياري، ومعظمهم يكتفي بحفظ القاعدة دون إجراء أي نوع من الربط.
بالعودة إلى فيثاغورس، واختتامًا للمقالة، فكر قليلًا إن كنت قد أعطيت الرياضيات فرصة حقيقية للتعلم والفهم، وصدقني، لو كانت المدارس ستقدم لك الرياضيات على طبق آخر غير حفاض الأطفال، لعرضت لك -بدلًا من وضع علاقة فيثاغورس بالخط الكبير على السبورة وأمرك بحفظها- هذه الصورة المتحركة:
 ملاحظة: هذا ليس ببرهان وإنما توضيح رائع
ملاحظة: هذا ليس ببرهان وإنما توضيح رائع
محتوى متعلق
يوجد كتاب قصير يتحدث عن ذات القضية بطريقة رائعة، من تأليف Paul Lockhart، يمكنك تحميله بصيغة PDF من
هنا
(بالإنجليزية).